The world of quantum computing continues to advance rapidly, challenging classical computational boundaries. A collaborative effort involving researchers from Freie Universität Berlin, University of Maryland, and Google AI has led to groundbreaking developments in estimating free Hamiltonian parameters in bosonic excitations. This endeavor, as detailed in a recently pre-published paper on arXiv, aims to improve the precision of quantum simulations that remain largely unattainable for classical computers.
The significance of this study cannot be overstated. Accurate Hamiltonian characterization is essential for effective quantum simulations, especially in tasks that would exponentially benefit from quantum mechanics’ inherent capabilities. It is within this framework that the researchers sought to enhance the experimental calibration of superconducting quantum systems.
Jens Eisert, the lead author of the study, recounted the genesis of this research during a conference in Brazil, where the extensive challenges faced by the Google AI team in calibrating their Sycamore quantum chip were first revealed. Initial insights led Eisert to believe that the complexities could be readily solved. However, upon deeper investigation, it became apparent that accurately identifying the Hamiltonian products from existing data would not be straightforward. “The crucial difficulties stemmed from the inability to recover the frequencies of the Hamiltonian operator correctly,” he noted.
This realization propelled the researchers to collaborate with brilliant minds, notably Ph.D. students Ingo Roth and Dominik Hangleiter, leading to the exploration of superresolution techniques. Although they initially found theoretical solutions, translating these into the realm of large-scale experimental application took time and effort.
The multidisciplinary nature of this project played a pivotal role in its success. Additionally, their experimental lead, Pedram Roushan from the Google AI team, provided invaluable data and remained resolute throughout the years of research. The culmination of their efforts revealed a robust method for Hamiltonian learning, which was unconventional yet innovative.
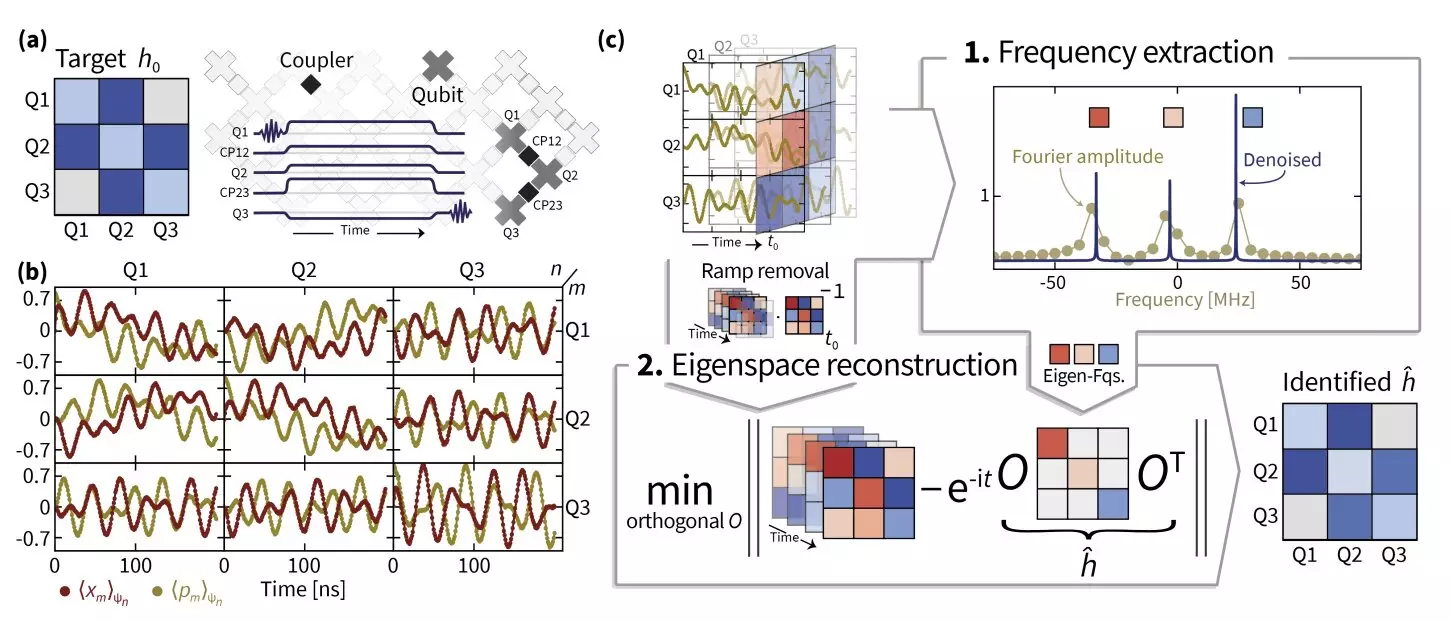
The researchers employed multiple advanced techniques, utilizing superresolution to enhance eigenvalue estimation, thereby obtaining accurate Hamiltonian frequencies. They further implemented manifold optimization, which helped recover the eigenspaces of the Hamiltonian operator. This optimized approach paves the way for practical applications, transforming abstract mathematical concepts into real-world implementations.
One of the standout techniques introduced in their studies is TensorEsprit, an innovative approach designed to achieve super-resolution effectively. By amalgamating this with manifold optimization, the researchers achieved robust identification of Hamiltonian parameters, successfully applying these techniques to systems involving up to 14 coupled superconducting qubits across two Sycamore processors.
Such advancements underscore the researchers’ emphasis on understanding Hamiltonian learning’s broader implications. The iterative process of refining these techniques proved crucial as they unraveled the complexities and challenges of applying theoretical frameworks to practical data. Their findings also highlight a broader trend in quantum research: the daunting difficulties associated with Hamiltonian learning and why so few publications in the field depict available data.
Looking ahead, Eisert and his colleagues are keen on scaling their methods further and exploring their applicability to interacting quantum systems. They plan to extend their research to utilize tensor network methodologies in natural settings, such as those comprising cold atoms, an area previously explored by physicist Immanuel Bloch. These exciting directions could redefine high-precision quantum simulations and analog quantum systems characterization.
Eisert notes the importance of having a precise understanding of a Hamiltonian operator, a topic often brushed aside in quantum mechanics. Traditional assumptions hold that Hamiltonians are known; however, the complexity of real-world systems frequently leads to unforeseen challenges. Accurately inferring the Hamiltonian from experimental data is not merely an academic exercise; it represents a critical step toward harnessing quantum technologies effectively.
The implications of this research extend beyond theoretical understanding; they are set to inform innovative technologies in quantum computing and related fields. By facilitating detailed characterization of analog quantum simulators, this work serves as a springboard for further exploration into high-precision quantum systems.
As Eisert states, “Analog quantum simulation facilitates a fresh perspective on complex quantum systems and materials,” reinforcing the potential for laboratory recreations to offer unprecedented insights into the underlying principles governing our universe. The intersection of mathematics, physics, and technology thus represents not just a future avenue of exploration but a profound transformation in how we understand quantum mechanics and apply its principles in the real world.

Leave a Reply